
Remark: here, the Cauchy stress tensor is denoted σ (instead of τ as it was in the general continuum equations and in the incompressible flow section). While individual fluid particles indeed experience time-dependent acceleration, the convective acceleration of the flow field is a spatial effect, one example being fluid speeding up in a nozzle. Though the flow may be steady (time-independent), the fluid decelerates as it moves down the diverging duct (assuming incompressible or subsonic compressible flow), hence there is an acceleration happening over position.Ī significant feature of the Cauchy equation and consequently all other continuum equations (including Euler and Navier–Stokes) is the presence of convective acceleration: the effect of acceleration of a flow with respect to space. These paths are the integral curves whose derivative at each point is equal to the vector field, and they can represent visually the behavior of the vector field at a point in time.Īn example of convection. In particular, the streamlines of a vector field, interpreted as flow velocity, are the paths along which a massless fluid particle would travel. Studying velocity instead of position makes more sense for a fluid, although for visualization purposes one can compute various trajectories. This is different from what one normally sees in classical mechanics, where solutions are typically trajectories of position of a particle or deflection of a continuum. Once the velocity field is calculated, other quantities of interest such as pressure or temperature may be found using dynamical equations and relations. It is usually studied in three spatial dimensions and one time dimension, although two (spatial) dimensional and steady-state cases are often used as models, and higher-dimensional analogues are studied in both pure and applied mathematics. It is a vector field-to every point in a fluid, at any moment in a time interval, it gives a vector whose direction and magnitude are those of the velocity of the fluid at that point in space and at that moment in time. The solution of the equations is a flow velocity. 13 Navier–Stokes equations use in games.
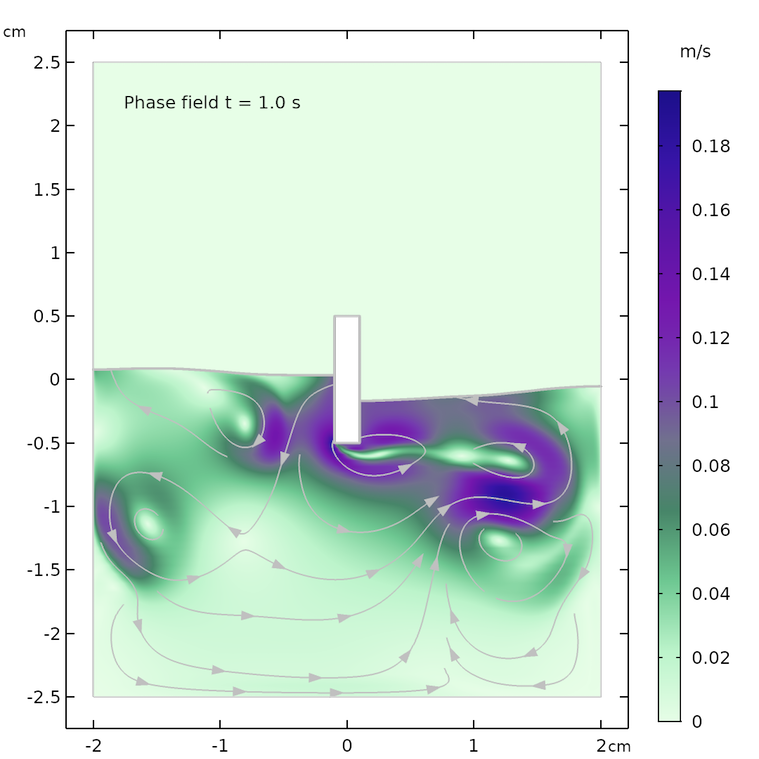

The Navier–Stokes equations are also of great interest in a purely mathematical sense. Coupled with Maxwell's equations, they can be used to model and study magnetohydrodynamics.

#Comsol 5.3 discretization of fluids full#
The Navier–Stokes equations, in their full and simplified forms, help with the design of aircraft and cars, the study of blood flow, the design of power stations, the analysis of pollution, and many other things.
They may be used to model the weather, ocean currents, water flow in a pipe and air flow around a wing. The Navier–Stokes equations are useful because they describe the physics of many phenomena of scientific and engineering interest. As a result, the Navier–Stokes are a parabolic equation and therefore have better analytic properties, at the expense of having less mathematical structure (e.g. The difference between them and the closely related Euler equations is that Navier–Stokes equations take viscosity into account while the Euler equations model only inviscid flow. They arise from applying Isaac Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term-hence describing viscous flow. They are sometimes accompanied by an equation of state relating pressure, temperature and density. The Navier–Stokes equations mathematically express conservation of momentum and conservation of mass for Newtonian fluids. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). In physics, the Navier–Stokes equations ( / n æ v ˈ j eɪ s t oʊ k s/) are certain partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes.


 0 kommentar(er)
0 kommentar(er)
